CHAPTER THREE

The Minus First Law

Dad died. He had a good run, ninety-six years. The last few years were tough, after strokes battered his old brain. He lived with Lois, my stepmom, at their home in Connecticut, but she had to hire someone to help care for him. Dad couldn’t really converse, but his spirits were still high. When Emily and I visited him and Lois, he thrust his fist up, grinning rakishly, and exclaimed in a hoarse whisper, “Hooray for you!”

I expected Dad’s death for years, even hoped for it, for Lois’s sake, and his. But it still rocks me when it comes. My sister Martha chokes up when she calls to tell me, and I choke up too, mirror neurons or whatever doing their job. I feel grief and surprise at my grief. Now that he’s gone, death sits amid the onrush of my thoughts like a black stone, opaque and immovable. Am I grieving for him or for myself, my own inevitable end and the end of all I love? All the above, I suppose.

The pandemic prevents me and my siblings from meeting for a memorial service, so I retreat into my quantum cave. What else can I do? I’ve temporarily set aside Susskind’s Theoretical Minimum after deciding that I need a better grounding in math, better than I’m getting from Wikipedia and “Math Is Fun.” Without calculus, I can’t grok partial differential equations such as the Schrodinger equation, which lets you track electrons and other particles. Following the recommendation of one of my advisors, I’m studying Quick Calculus by physicists Daniel Kleppner and Norman Ramsey. It is a classic primer, in print since 1985. 

Quick Calculus is tough at first. The title becomes a taunt. Quick? Not in my case. But gradually I make headway. Kleppner and Ramsey devote Chapter One to “A Few Preliminaries”: sets, functions, graphs, linear equations, quadratic equations, trigonometry, logarithms. Unlike Susskind, whose approach is sink or swim, Kleppner and Ramsey make sure you understand something before moving on. After giving you a tutorial on, say, trigonometry, they test your knowledge by giving you a problem. If you can’t solve it, you can skip ahead to find the answer, along with an explanation of how it is derived. Pardon the pun.

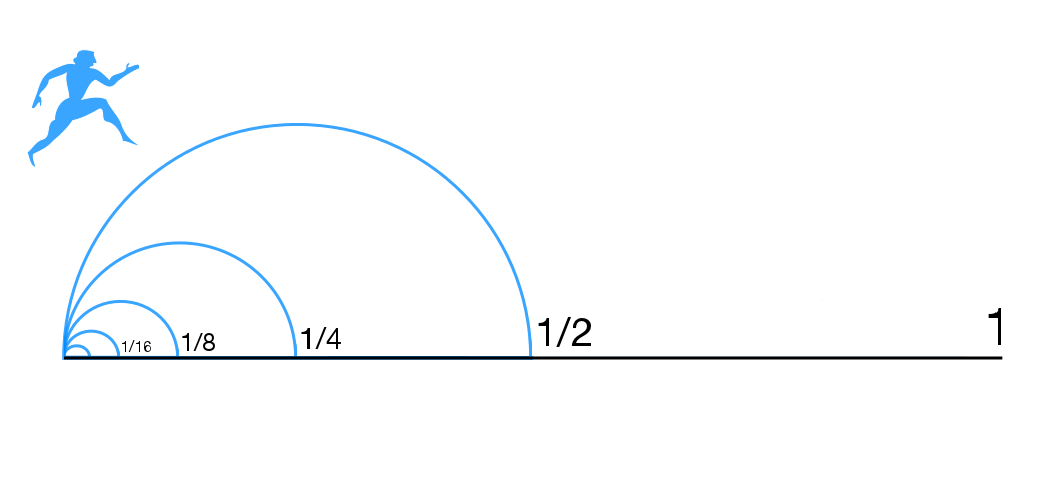
Chapter Two, “Differential Calculus,” begins with limits, which are “at the heart of calculus.” I love limits! They are chock-full of metaphorical potential. Limits are related to a paradox posed by the ancient Greek guy Zeno. He says: Let’s assume you’re trying to walk from A to B. Before you get to B, you have to go half that distance, or B/2. Before you get to B/2, you have to go half that distance, B/4; before you get to B/4, you have to go half that distance, and so on. The paradox applies to time, too. It takes infinite moments to get from A to B. So how can you get anywhere? How can anything happen?

The answer lies in limits. As you keep subdividing the distance between A and B, taking half of it, then half of that, and half of that, those distances quickly approach zero. And when you add these increasingly tiny distances, or infinitesimals, they produce a finite distance. This phenomenon, in which an infinite number of quantities produce a finite quantity, is crucial to mathematics and physics. It is the essence of calculus, of derivatives and integrals, of differential equations, all of which help us track arrows, rockets and electrons. And it all traces back to Zeno’s paradox.

I remember almost nothing from the calculus course I took in college 40 years ago. But I do recall being awed by how limits, and infinitesimals, allow you to calculate the slope of a curve at any given point, giving you the rate of change of something tracked by that curve. This procedure, the basis of differential calculus, seemed like magic, sleight of hand.

As Klepper and Ramsey walk me through the logic behind differential calculus, I’m awestruck all over again. Let’s say you have a cartesian grid with a vertical y axis and horizontal x axis. You have a simple function, like y equals 3 times x, that is, y = 3x, and you want to calculate its slope. The mnemonic for calculating slope is “rise over run.” That is, you take the rise along the vertical y axis and divide by the corresponding run along the x axis. If you plot y = 3x, you can take any rise and divide it by its corresponding run, and you get the same number, 3, a constant. That is the slope, or rate of change, of the function. That slope would correspond, say, to a car rolling at a constant speed of 3 meters per second.

But now let’s say you want to find the slope of the function y = x², which generates a curve, a parabola. The slope of a parabola constantly changes. You want to find the curve at the point where x = 3 and y = 9. How do you get the slope at a single point, which by definition has no distance, no rise or run? That’s like dividing 0 by 0, which is mathematically meaningless.

Here’s what you do. You pick two values of x equidistant from where x = 3, say 1 and 5. You draw a line between their corresponding points on the curve and get a slope, equal to rise over run. You keep moving those values of x closer and closer to x = 3, and you keep dividing the increasingly tiny rises by the increasingly tiny runs. You are not dividing 0 by 0, which generates meaningless results; you are dividing infinitesimal rises by infinitesimal runs. The limit of that slope as the rises and runs approach zero is the slope at x = 3. Abracadabra. This trick is the basis of differential calculus, which allows us to track changes, micro and macro, happening within and without us as time passes.

Limits are called convergent if they get closer and closer to one particular number, which gives you, say, the slope of y = x² at x = 3 (which happens to be 6). Limits are divergent if they never approach a single number. Limits might veer back and forth between different values or fly off to infinity.

Quick aside on the so-called quantum Zeno effect, which was first described in the 1970s and has provoked lots of research and commentary. Quantum mechanics predicts that if you keep checking the status of, say, a radioactive particle, you collapse the particle’s wave function and hence delay its decay. The quantum Zeno effect recalls the old aphorism, A watched pot never boils. The difference is that the watched-pot effect is subjective and the quantum Zeno effect objective. Supposedly.

It would be nice if the quantum Zeno effect could be harnessed to keep our bodies from decaying. Of course, senescence isn’t the same as radioactive decay, and monitoring each of the gazillion molecules in our bodies would be cumbersome. As a fallback, you could seek immortality by paying close attention to each of the infinite moments between you and death. Now! Now! Now! Just try to forget that that an infinite number of infinitesimal moments adds up to a finite moment.

Memento Mori

Reasoning that reminders of death make us pay closer attention to life, I have decorated my apartment with memento mori. These include a ceramic skull with red LED eyes, pinned to the wall of my living room; a tin, dancing skeletal couple in my front hall; a cushion that shows a white whale, jaws agape, about to devour a tiny, unsuspecting sailboat. Emily gave me the cushion and dancing skeletons.

These items seem superfluous lately, because everything serves as a memento mori. The blue barge moving slowly up the Hudson, the budding trees in the park, the bright green grass. Not to mention the daily Covid death count, which I check in The New York Times every morning. Everything says, Everything ends, nothing stays the same. I’m my own memento mori. I have an achy tooth, a sore Achilles tendon, an odd lump on my left shoulder. I’ve been misspelling and mispronouncing words lately. Entropy is wearing me down.

Physics is an especially brutal memento mori. It’s hard enough dealing with our own end, and the ends of those we love. Physics forces us to contemplate the extinction of the solar system, when the Sun bloats like an old, diabetic drunk; and beyond that the demise of the entire universe, when heat death slowly crushes any lingering remnants of life, mind and meaning in the increasingly cold, dark cosmos. The last thing to go is time itself. Nothing can happen, there’s no change. No need for calculus anymore! So says the second law of thermodynamics, the most totalitarian principle of physics. 

Physics has stripped us of our traditional spiritual consolations: a loving God and an afterlife, in which the good are rewarded and the wicked punished. And in return, physics gives us… what? We can take comfort from the lovely laws of nature. Stephen Hawking, at the end of A Brief History of Time, says once we discover the final theory, which spells out the laws of nature, we’ll know “the mind of God.” That was a cruel joke. Hawking was an atheist and a kidder. If you read Brief History carefully, you realize that he believes physics has eliminated, or will soon, any need for a divine creator. Funny, not funny.

But physicists are human; they fear death too. I suspect physicists’ awareness of mortality, of transience and loss, underpins their obsession with two closely related concepts: symmetry and conservation. Something is symmetric if it remains unchanged when you rotate it, flip it, substitute one part for another or otherwise transform it. Something is conserved, similarly, if it remains constant while undergoing changes, such as moving forward or backward in time. Physicists love showing that things stay the same if you look at them the right way.

Protons and sulfur atoms exhibit symmetry, in that you can substitute one proton for another, and one sulfur atom for another, without changing the results of your experiment. Humans, unlike protons and sulfur atoms, are not interchangeable; hence the difference between so-called hard sciences, such as physics and chemistry, and soft sciences (which are actually much harder), such as psychology and anthropology. Each human being is unique, irreplaceable, a truth we feel most acutely when someone close to us dies.

As I turn the black stone of death this way and that, trying to see it in a positive light, it occurs to me that death is a MacGuffin. That’s a filmmaking term for something that propels a plot, like the Maltese Falcon in The Maltese Falcon or the Ark of the Covenant in Raiders of the Lost Ark. The MacGuffin can be an object of desire or fear or both. The MacGuffin motivates characters, sets them in motion, so the audience can watch how they act and learn who they are.

The death of an individual serves as the MacGuffin in cheesy whodunnits, like Murder She Wrote. Death, with a capital D, also drives the plot of this cosmic whodunnit in which we find ourselves. What’s the point of living if we’re doomed from the start? Can we transcend our mortality? And who wrote this shitty screenplay, anyway? The plot meanders, there’s no resolution in sight. The writer strings us along, keeps us hanging. We hope for an answer even though, deep down, we suspect there is none. We’re in one of those postmodern anti-stories that has no plot, no point. Pointlessness is the point.

Quantum mechanics is a MacGuffin, too. It’s a mystery, a plot device that absorbs legions of scientists, philosophers and clueless science writers. Maybe quantum mechanics and death are two aspects of the same meta-MacGuffin. Maybe if we solve one, we solve the other. [1]

Chain Rules 

My progress through Quick Calculus decelerates as the book’s drag coefficient increases. The book gives you rules for differentiating functions such as quadratic equations, sines and cosines, exponents and logarithms. Differentiating a function means finding its slope, or rate of change, at a particular point. Then you learn how to differentiate compound functions, which are functions made of functions, via the chain rule: you break the equation into chunks that you differentiate separately. Applying the chain rule is tedious, but when I pull it off, I get a spurt of pleasure, just enough to keep me going.

An irony occurs to me: the rules for calculus are simple, precise and logical compared to the rules for composing and decoding English sentences. We follow hideously complicated, arbitrary and unstable chain rules whenever we converse, and yet we chatter easily, blithely, because our innate language skills are vastly superior to our math skills. When I chitchat with Emily, my thinking is usually pretty fast, as psychologist Daniel Kahneman defines it in Thinking, Fast and Slow. Fast thinking is intuitive, reflexive, automatic, even unaware. When I work on chain-rule problems, my thinking is painfully conscious, deliberate, slow.

I think that’s how Kahneman distinguishes fast and slow thinking. I never actually read Thinking, Fast and Slow, although Dad bugged me to for years. Dad loved Kahneman’s book, and he knew I’d love it, too. He mailed the book to me and kept asking if I’d read it. I had a stubborn resistance to his book recommendations, proportional to his insistence. Why is that? A carryover, perhaps, from my youth, when I disdained my father’s bourgeois values, which of course I’ve come to share. Should I read Thinking, Fast and Slow now, for Dad’s sake? To honor him? No, too late. [2]

Natural selection has designed our brains to carry out tasks with minimal conscious, deliberate, effortful cogitation. Ideally, we learn to perform like clever automatons, adhering to the shut-up-and-calculate principle—and of course to the law of laziness. But I’m having a hard time getting past the slow-thinking stage of calculus. I’m impatient. When I get stuck on an exercise in Quick Calculus and skip over it, I feel guilty. This is happening more often as I approach the end of the book, which assumes that I remember what came before. Often, I don’t remember. I get frustrated and move on, hoping, usually in vain, that the next section will be easier.

My favorite rule for taking a derivative, which is represented by d, is d(xⁿ) = n times x to the power of n-1. Example: d(x³) = 3x². It’s my favorite rule because it’s the one I reliably remember. I struggle with the fundamental theorem of calculus, which connects derivatives and integrals. Derivatives are the product of differentiation, and they give you the slope of a curve at a given time t. Integrals, the product of integration, give you the area under the curve between two points—which typically stand for two times, like t = 0 and t = 1.

I know, not from Quick Calculus but from other readings, that integration is crucial to quantum mechanics; it is the basis of path integrals, a method refined by Feynman. The area under the curve of a wave function between t = 0 seconds and t = 1 seconds helps you calculate the probable paths of a particle in that period. The probabilities must add up to one, because something must happen when you look.

Limits are crucial to integrals, just as they are to derivatives. Let’s say you want to know the area under the curve of a function between two points, corresponding to two different times. “Area under the curve” means the area between the curve and the horizontal axis, which represents time, bounded by the points a and b. You get an approximation of the area by chopping it up into rectangles that extend from the curve to the horizontal axis. As the horizontal width of the rectangles approaches zero, the number of rectangles approaches infinity. The limit of this process is the area under the curve of the function, or its integral.  

I try to see integrals as anti-derivatives, but my powers of visualization keep failing. It’s as though I’m trying to turn a three-D object inside-out in my head, like when I tried to help Emily put her king-sized duvet back in its freshly washed cover. She had watched an online video on how to perform this task. You roll the duvet up into a cylinder; then you turn the cover inside-out, reach into it, grab the edge of the duvet and pull it into the cover, unrolling the duvet as you go. I had a hard time seeing the logic, so I bullied Emily into letting me stuff the duvet into the cover and shake it out. After the duvet ended up all lumpy, we did it her way, which worked.

I go over and over the fundamental theorem of calculus, but it keeps slipping away, because I can’t see it. Trying to integrate an equation, I feel a tightening in my chest. My breathing becomes shallow. I give myself pep talks, I’m doing this, I’m getting this, while also thinking, I don’t get this, it’s too hard. I have performance anxiety even though I’m just lying on a couch in my living room with no one watching.

I whine about Quick Calculus to Jim Holt, one of my advisors, who has a master’s in mathematics and has written a lot about quantum mechanics. I tell him that I’m okay with derivatives, lousy with integrals, and I keep forgetting what I’ve learned. Holt tells me not to worry, that happens to everyone; he mentions famous philosophers of physics whose math is shaky. Holt adds that integrals are harder to get than derivatives; derivatives are just an “algorithm,” whereas “integrals are art.” Holt mastered integrals when he taught them in grad school. He could solve hard integration problems on the blackboard as sharp-eyed students watched, waiting for him to fuck up.

Hawking supposedly said that physicists are washed up by 30. Hawking meant that physicists can no longer do advanced, creative physics, but still, Hawking’s assertion sobers me. So does googling “learning math in your 60s.” People on Reddit complain about how hard it is to learn math and physics in your thirties. [3]

Dying Like a Physicist

I’m in a park studying Quick Calculus. It’s Saturday, and the park is packed with kids racing around on scooters and kicking balls. Masked and unmasked parents look on fondly or anxiously—when they’re not staring at their phones. I try to do integration exercises, but I’m distracted by the activity around me.

These clamorous children, beloved by their parents, can be viewed as objects of a certain size and mass expending energy and being accelerated by varying forces along twisty trajectories. The children are also computational devices whose calculations are underpinned by physical processes, such as the transport of chemicals across synapses.

This is, for me, a novel way of looking at the world. Is it a good way? Is it better than my ordinary, common-sensical, folk-psychological perspective, which looks at these kids as creatures with minds, emotions, motives and all the rest? David Hilbert, the mathematician after whom the space is named, says math requires more imagination than poetry. Many physicists share Hilbert’s snooty mindset. They agree with Plato that the highest reality is mathematical. God is a geometer and so on.  

Some physicists, like Andrei Linde, doubt this assumption. I met Linde in 1990 at a symposium in Sweden on the “birth of the universe.” Hawking and other bigshots were there. Linde, who would soon leave Russia for Stanford, co-invented a popular theory of cosmic creation called inflation, which says the universe sprang from a “quantum fluctuation.” Quantum mechanics decrees that even in the emptiest void, particles are always popping into existence; one of these “virtual particles” gave rise to our universe. Inflation implies that our universe is just a fleck of foam in a vast, frothy multiverse with no beginning or end.

In Sweden Linde entertained us not only with his extravagant cosmic conjectures but also with sleight of hand. His best trick was holding two wooden matches, one atop the other, on the palm of his hand; the top match hopped up and down as though tugged by an invisible string. When his brilliant colleagues demanded to know how he did it, Linde growled “quantum fluctation” with what sounded like a parody of a Russian accent: “kvan-toom flook-choo-a-shoon.” Funny. But Linde was a tortured soul. He muttered to me, “I’m depressed when I think I will die like a physicist.” Yes, because physics leaves too much out. It leaves out love and fear and death and other things that matter.

What explains our peculiar human reality, with its crazy mix of good and bad, beauty and ugliness, joy and suffering? What’s the meaning of our existence? We want more than a physical description. We’re looking for consolation, assurance that we matter, which physics in its present form can’t give us. That, I believe, is what Linde meant when he said, “I’m depressed when I think I will die like a physicist.”

Linde said something else that stuck in my head. He speculated that our universe was created by beings in another universe; the laws of nature, which he and other physicists are trying to decipher, might contain a message from our cosmic creators. When I asked what the message might be, Linde replied mournfully, “It seems we are not quite grown up enough to know.”

I’ll take a stab at it. I’ll assume that the message is posthumous; our cosmic godparents composed it shortly before they expired. Their message is that we matter, and everything will be all right, our pain and fear will not be in vain, as long as we care for each other, treat each other with kindness. Our godparents couldn’t follow this advice; that’s why they vanished. But they lived long enough to create us and impart this message to us, so we have a shot at enduring joy.

Yes, our godparents will give us a nice liberal-progressive message: Be kind. Unless the message is “Hunh?” or simply a question mark: “?” Our cosmic ancestors would be letting us know that they’re puzzled too; they never figured things out. Wait, here’s another possibility. Their message to us might be the equivalent of Ψ, the symbol for the wave function. Ψ is both an answer and a question. The answer/question eggs us on, keeps us going, tantalizes us with the promise of a final revelation that never quite comes. You can’t ask for a better MacGuffin. 

Conservation of Information

I’m done, for now, with Quick Calculus. I need to get back to physics. Rather than immediately returning to Susskind’s book on quantum mechanics, I’m reading his Theoretical Minimum book on classical physics. This, plus Quick Calculus, will surely give me the background I need to make more sense of quantum mechanics. And it does, sort of. Susskind starts with Aristotle, who postulated that force is required to keep a mass moving. This is a reasonable assumption in situations where friction, also called the drag co-efficient, is high.

Newton perceived the ideal, abstract truth underlying the messy reality of our gritty, viscous world. He realized that inertia is conserved, and he expressed this truth in clear, simple mathematical formulas, like force equals mass times acceleration, or F = ma, which can also be written as F = m x dv/dt, with v standing for velocity, since acceleration is the rate of change of velocity. Susskind reviews these laws, imparting a little calculus along the way. This material doesn’t totally baffle me; Quick Calculus has helped.

Susskind says 18th and 19th century mathematicians seem almost “clairvoyant” in anticipating concepts of quantum mechanics. Joseph-Louis Lagrange and William Hamilton came up with mathematical methods for tracking how the energy of a system changes. The Lagrangian is the difference between an object’s kinetic and potential energy, and the Hamiltonian is the sum of kinetic and potential energy. The potential energy of a rock teetering on the edge of a cliff and of a rocket sitting on a launchpad turns into kinetic energy as the rock falls and the rocket rises.

Hamiltonians and Lagrangians make the world easier to model, predict, manipulate. The smelly, noisy, gritty, multi-colored, bittersweet, delightful, dangerous world. But are we seeing the world more clearly when we model it in these abstract ways, or are we seeing past it? Science is reductionist by definition; it reveals that complicated effects have simple causes, such as natural selection, gravity, the double helix, action potentials. The reductions leave out a lot. The question is, are these omissions important?

Hamiltonians and Lagrangians are hard for me to grasp. The terms resemble mystical incantations, like “Holy Spirit” or “Atman.” Except I can dismiss mystical terms as mumbo jumbo, whereas Lagrangians and Hamiltonians work, they get shit done. They help engineers design spaceships that land on Mars and H-bombs that blow up. Lagrangians and Hamiltonians are the antithesis of mumbo jumbo. My poor brain, desperate for meaning, seizes on any association to make the terms less abstract. I personify terms: the Hamiltonian is stuffy, wearing the stiff, black and white garb of a Puritan. The Lagrangian is a Musketeer, a rakish French dandy in a plumed hat.

I try hard to grasp the harmonic oscillator, which Susskind calls “by far the most important simple system in physics,” including quantum mechanics. He provides a formula for the motion of an oscillating object: x(t) = sin wt, with x being the position of the oscillating object, t being time and w, a constant, being proportional to the rapidity, or frequency, of the oscillation. sin stands for sine. You can differentiate this formula to get the velocity and acceleration of the object at any given time. This is classical, sensible oscillation, like that of a swinging pendulum, vibrating string or beating heart.

Quantum mechanics has its own version of harmonic oscillation, which involves Hamiltonians. The wave function, Ψ, oscillates, but it is a mathematical entity, a hybrid of real and imaginary numbers, pulsing in a mathematical realm tangential to ours. And this strange thing, Ψ, might be the spark--the kvan-toom flook-choo-a-shoon--that ignited the big bang, the cosmic conflagration in which we burn.

Another idea that jumps out at me from Susskind’s classical-physics book is “conservation of information,” which he calls “the most fundamental of all physical laws.” It says that information is never destroyed; it is always preserved, in one form or another. The universe, at this moment, bears the imprint of everything that has ever happened.

Conservation of information is more fundamental, Susskind says, than Newton’s first law (motion is conserved), the first law of thermodynamics (energy is conserved) and what is sometimes called the zeroth law of thermodynamics (if systems A and B are each in equilibrium with C, then A and B are in equilibrium with each other). Hence Susskind calls conservation of information the “minus first law.”

The minus first law encompasses the principle of determinism, which holds that if you know the current state of a system, you know its entire past and future. Here is how Susskind puts it: “The conservation of information is simply the rule that every state has one arrow in and one arrow out. It ensures that you never lose track of where you started.” The French polymath Simon-Pierre Laplace spelled out the implications of determinism over 200 years ago:

An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes.

This omniscient “intellect” has come to be known as Laplace’s demon. Susskind insists that quantum mechanics, although not deterministic in the same way as classical mechanics, still conforms to the minus first law. This claim is controversial. In the 1980s Stephen Hawking challenged the minus first law, claiming that black holes destroy information; the arrow goes in, but it doesn’t come out. Susskind rebutted Hawking in technical papers and a pop-physics book, The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics.

I can’t follow Susskind’s explanation of why quantum mechanics, which is probabilistic, is also deterministic, meaning that each quantum state has one arrow coming in and one going out. Doesn’t a quantum state describing an electron yield many “out” arrows, corresponding to all the electron’s possible paths? Maybe Susskind means that quantum mechanics becomes deterministic if you’re tracking many particles, which collectively adhere to the law of laziness, a.k.a. principle of least action. But I’m not sure. I must be missing something.

I also have a fussy technical objection to conservation of information, which comes from my knowledge of information theory. This theory, which underpins all our digital technologies, arguably has the lowest recognition/impact ratio of any idea in history. It was invented by mathematician Claude Shannon in the 1940s when he was working at Bell Laboratories. Looking for a way to quantify data passing through phone lines and other channels, Shannon devised a precise, mathematical definition of information. The potential information in a system, Shannon proposed, is related to its entropy, which is a measure of all the ways in which the components of a system can be shuffled; more possible shufflings mean more possible messages. But more entropy also means more potential randomness, or noise, that can swamp messages.

Shannon’s definition might make information sound like an objective, physical phenomenon, but it’s not; information is in the eye of the observer. Shannon introduced information theory in a 1948 paper titled, “A Mathematical Theory of Communication.” I italicize Communication to emphasize that information, as defined by Shannon, presupposes the existence of minds that can send and receive messages. Hence information is intrinsically subjective.

Also, when I interviewed Shannon in 1989, he told me that the information in a message is proportional to its potential to “surprise” a recipient. If I tell you something you already know, like the formula for a harmonic oscillator, I’m not giving you information. If all of us vanish, all the information in our computers would vanish too; the bits would become just peculiar arrangements of matter. For these reasons, I get irritated when physicists like Susskind try to co-opt the concept of information and turn it into something purely physical. Information, stripped of its human context, is as meaningless as money. 

Conservation of information, the minus first law, also defies common sense, and not in a good way. I can’t even recall what Emily said this morning to make me so upset with her. I can tell you a “story,” as my friend Jim McClellan, a postmodern historian of science, would put it. But our knowledge is always incomplete. We can’t ever know what really happened, or even what’s happening right now. Memories are unreliable, records fragmentary, and things fall apart, as dictated by the second law of thermodynamics. So how can physicists say that information is “never lost?” They aren’t talking about human memory, but still.

I’d love to believe the minus first law. It implies that the universe will bear the imprint of our lives forever. Long after our sun and even the entire Milky Way have succumbed to heat death and flickered out, beings with the powers of Laplace’s demon, such as our superintelligent machine descendants, could in principle reconstruct the lives of every person who has ever lived. Like my father.

It’s been more than a week since his death, and I’ve moved on. Sort of. My father, who was a big kidder, persists as a mischievous force field subtly distorting my perceptions of the world. My brother and three sisters and I can’t meet in person to remember him, so we assemble via Zoom. Our memories and judgements are fragmentary and divergent. How did Dad treat our boyfriends and girlfriends back in the 1970s? Was he kind or snobby? How did Dad deal with our biological mother’s radical-feminism phase, or her long death from cancer in the 1980s? We cannot agree on what our father really did or who he really was, and we can only argue about what we experienced. Most of Dad’s life is unknown to us.

We invented God to watch us and remember everything about us, so our lives matter. If you don’t believe in God, you can believe in the minus first law, conservation of information, which decrees that the universe records everything about us; it never forgets. Long after my father has vanished, he will endure in some form. We all will. Wouldn’t it be nice to think so.

As my siblings and I are winding down our Zoom memorial, I raise my fist and say, “Farewell Dad! Hooray for you!”

Notes

1. Terror-management theory, proposed several decades ago by a trio of psychologists, says fear of death underpins many of our convictions and hence actions. We cling to our convictions—religious, political, whatever--more tightly when reminded of our mortality, especially when those convictions connect us to something transcending our puny, mortal selves. Terror-management theory offers insights into physics as well as into our pathologically polarized country.

2. I ruminate over my ambivalence toward my father and bourgeois values in “A Pretty Good Utopia,” chapter nine of my book Mind-Body Problems.

3. A reader, Najum Mushtaq, informs me that Paul Dirac, before Hawking, said physicists are washed up by 30. “In fact, the reticent grand Bristolian master said it with an uncharacteristically poetic flourish:

   “Age is, of course, a fever chill
   That every physicist must fear.
   He's better dead than living still
   When once he's past his thirtieth year.”

    The poem appears on page 137 of The Strangest Man: The Hidden Life of Paul Dirac, Mystic of the Atom by Graham Farmelo. Thanks Najum!

Table of Contents

ABOUT MY QUANTUM EXPERIMENT

INTRODUCTION
Old Man Gets More Befuddled

CHAPTER ONE
The Strange Theory of
You and Me

CHAPTER TWO
Laziness

CHAPTER THREE
The Minus First Law

CHAPTER FOUR
I Understand That
I Can’t Understand

CHAPTER FIVE
Competence Without Comprehension

CHAPTER SIX
Reality Check

CHAPTER SEVEN
The Investment Principle

CHAPTER EIGHT
Order Matters

CHAPTER NINE
The Two-Body Problem

CHAPTER TEN
Entropy

CHAPTER ELEVEN
The Mist

CHAPTER TWELVE
Thin Ice

CHAPTER THIRTEEN
Irony

EPILOGUE
Thanksgiving

THANKS

DISCUSSION