CHAPTER NINE
The Two-Body Problem
As election night drags on, I feel bad not in an abstract, intellectual way but in a visceral way, as though someone socked me in the gut. I cycle between rage, denial and despair, just as I did when I finally knew my marriage was over. The morning after the election, I have to teach my “War & Science” seminar. The course is based on my book The End of War, which argues that war is neither innate nor inevitable; we can end it if we want to. It’s my duty to infuse students with optimism, but looking at these young faces on my laptop this morning, I’m in a bitter mood. I say, How could all the polls be so wrong—again! A student replies: Um, professor, I’m on a website that says Biden is still favored to win when all the votes are counted.
I begin to hope.
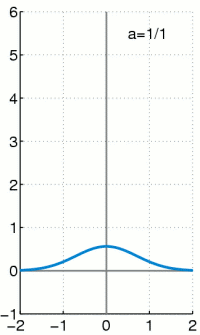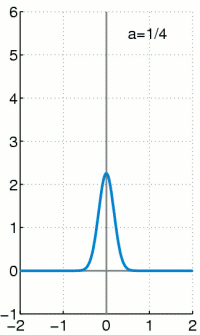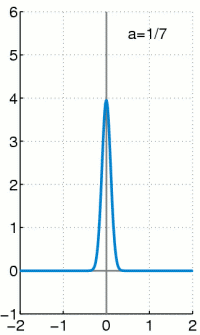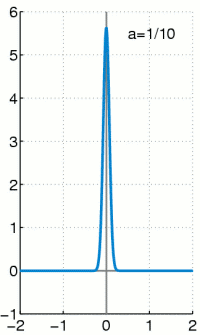
I welcome the distraction of PEP553. Professor Whittaker, Ed, is reviewing the Dirac delta function, which I find intriguing. Normally, even a stationary wave function is spread out along the x axis, corresponding to all the different probable locations of the particle. You integrate to get the area under the curve; that area corresponds to all the probable locations of the particle. The area must equal one, because the probabilities must add up to one; the particle must be somewhere when you look.
I found this animation of the Dirac delta function on Wikipedia. My PEP553 professor calls the function “mathematical skullduggery.”
But let’s say you just know the particle is in one spot. What function can represent that situation? And how do you integrate the area under that wave function if you’re talking about a single point? That’s like getting the area of a line. Paul Dirac came up with a solution to the puzzle. You postulate a curve that starts at one point on the x axis, goes up a certain distance and then comes back down to the x axis again to another point. If you integrate the curve, you get an area of 1.
Now you make the base of the curve smaller and smaller, while making its peak taller and taller, so the area of the curve remains one. If you keep doing that, you end up with something that isn’t quite a curve and isn’t quite a line; it is the limit of a curve as it approaches becoming a vertical line. It is an infinitely skinny, infinitely tall spike that somehow has an area of one.
The Dirac delta function is an odd, ad hoc mathematical invention. But it is widely used, because if you assume the function exists, you can do all sorts of stuff with it. It allows you to make the transition from the real world, in which you cannot measure time and space with absolute precision, to the abstract mathematical realm of precise points in time and space. Griffiths calls the Dirac delta function “an extremely useful construct in theoretical physics.” In class, Ed Whittaker describes it as “mathematical skullduggery,” a phrase I jot down with relish.
Several days after the election, my daughter Skye calls, crying. My heart sinking, I ask her what’s wrong, but she is crying because she’s happy. The Associated Press just called the race for Biden, and she wanted to share the news. To my surprise, I get teary too, and so does Emily when I tell her the news. Afterwards, I reflect again on the limits of physics. Physics explains a lot: the outrushing of the cosmos, the whirling of galaxies and planets, the shining of the Sun on the Hudson River this morning, the river’s tidal surges.
But physics can’t explain why, when I look beyond the river at Manhattan, I see the silver wedge of the Freedom Tower instead of the Twin Towers. Physics can’t explain what drove men to hijack planes and fly them into the World Trade Center in 2001. It can’t explain how that catastrophe turned my wounded country into a vengeful, warmongering monster. Physics can’t explain the fear and anger and hatred that perpetuates war.
I’m glad Biden won.
Conservation of Ignorance
In our next session of PEP553, Ed reviews more functions, useful ways of modeling different quantum behaviors. It’s hard enough keeping track of individual functions, but what really gives me trouble are nested functions, functions within functions. You might think of nested functions as being akin to familial relations, like the cousin of the brother of the grandfather. But that’s too straightforward. A better analogy would be the stockbroker of the priest of the music teacher.
Except I know what stockbrokers and priests are. The Dirac delta function and Hermitian operator have no objective correlative, certainly not in the way that stockbroker and music teacher do. The functions only make sense in their other-worldly quantum context. We try to grasp them, to link them to things with which we are familiar, but our efforts only take us deeper into abstraction and further from things moving around in the world. Our human world.
My cluelessness makes me think of my father. What was his state of mind toward the end, when he sat, slack-jawed, seeming to look at nothing? If I caught his eye, he’d smile and raise a fist, meaning, Hooray for you, which is what he’d say before he couldn’t even say that. Otherwise, when he wasn’t reacting to me, my stepmom or Emily, was he wandering among ancient memories? Or was he on the outskirts of oblivion, getting acclimated? Quantum mechanics says nothingness doesn’t exist; a side effect of uncertainty is that even the emptiest box seethes with “virtual particles” popping in and out of existence, generated by so-called creation and annihilation operators. I’m grateful to the physicists who coined these evocative terms. Maybe my father’s mind seethed with virtual thoughts springing from creation operators.
Ed has been talking about uncertainty. I ask if any physicists still think quantum uncertainty stems from the physical interference inevitably resulting from measurements of tiny things; to track an electron, you must bounce photons off it, disrupting its trajectory. Yes, all observations are disruptive, Ed replies, but uncertainty seems to be a part of the reality that quantum mechanics describes.
But what’s cool, Ed says, is that you can manipulate uncertainty; you can give up knowledge of one variable, increasing your uncertainty about it, to get more knowledge of another variable. This technique produces what are called “squeezed states,” which have been the focus of Ed’s own research. The Laser Interferometry Gravitational Wave Observatory, LIGO, employs squeezed states to detect gravitational waves, ripples in spacetime triggered by the collision of black holes and other cosmic cataclysms.
Reflecting on squeezed states later, I imagine them represented by the Dirac delta function, which you get by squeezing an ordinary function with both hands until it become an infinitely tall, skinny spike with an area of one. The function occupies a single value on the horizontal axis and all values on the vertical axis. You pay for absolute knowledge of one variable with utter ignorance of another. The more you know, the less you know; truth is a zero-sum game.
I have a friend with a gloomy Puritanical outlook who has proposed a law called conservation of misery: we pay for pleasure now with pain later. The uncertainty principle could be called conservation of ignorance, which is the flip side of conservation of information, which Leonard Susskind calls the minus first law. We clever, modern humans have accumulated a lot of information, which has helped us invent lots of cool stuff. What price have we paid for all our spiffy knowledge and inventions? What have we forgotten, or never learned, because it is hidden by our “knowledge”? Our ignorance is measured in that infinitely high spike of the Dirac delta function.
Hilbert Space and the South Pole
Only a few weeks of PEP553 to go, and Professor Whittaker is moving fast. He reviews topics we’ve gone over before, and he adds new ones: two-by-two matrices, projection operators, basis transformation, subspaces. Subspaces are spaces with finite dimensions contained within Hilbert space. Two-by-two matrices representing spin, called Pauli matrices, inhabit two-dimensional subspaces. “Subspace communication” is a staple of Treknobabble, but I’m guessing Star Trek’s subspace is as unrelated to mathematical subspaces as The Matrix is to matrices.
I try hard to get the concept of basis transformation, which seems important. In linear algebra, basis refers to a special set of vectors in a given vector space. Each vector has a certain length, and each is orthogonal to the others. You can combine these basis-vectors to form all other possible vectors in the vector space. If you choose your basis wisely, your calculations become easier. There are operators, Whittaker says, that transform one basis for representing quantum vectors into another, making the vectors easier to manipulate.
I think of basis as roughly equivalent to frame of reference or coordinate system. Just shift your frame of reference, and your calculations might become simpler; you might see things more clearly. Example: If you find the Fahrenheit temperature scale too clunky, you can shift to the Celsius scale, which makes 0 and 100 degrees the temperature at which water freezes and boils. That’s just a transformation of your units, which are analogous to the length of your basis vectors.
Modeling the solar system with Earth at the center works—Ptolemy could predict eclipses with his geocentric model--but it leads to all sorts of complications. Simply shift your frame of reference, putting the Sun at the center, and your model becomes much more straightforward and sensible. Remember, the vectors that model quantum happenings consist of complex numbers, and they dwell not in our three-dimensional world but in Hilbert space, which can have as many dimensions as you like.
Drifting into idle thought experiments, I imagine how I might model Emily in Hilbert space. I would dedicate a different dimension to each of her variables. Some correspond to her physical self, including shape, height, weight, hair color, scent, the sound of her voice. Other dimensions correspond to her psychological self, including emotional tendencies, aptitudes and deficiencies, likes and dislikes. Only a rapey creep, it occurs to me, would want to model his girlfriend in this way. And what good would a model of Emily do me, anyway? I still couldn’t predict and/or manipulate her actions for my benefit. Conservation of ignorance would still hold.
Another question: If I really understood Hilbert space, would I be less free to wax poetic about it? Would all those annoying technical details constrain me? No, the technical details would be even more inspiring, because they would be strange in ways I can’t imagine. Just as the South Pole, which I visited on an assignment for Scientific American in 1992, turned out to be strange in ways I could not imagine.
When a Navy ski-plane carrying me and three other journalists skidded onto the South Pole, we watched in astonishment as a young crewman stripped to his underwear and dashed outside for a minute or two. This ritual turned out to be mandatory for crew members arriving at the Pole for the first time. Another unexpected detail: Someone had marked the South Pole with a candy-striped column with a mirrored sphere on top, like the ones with which suburbanites adorn their lawns. A touch of the familiar to make this frigid, perilous place less forbidding.
When I visited the South Pole, it was mid-November, early summer, and the temperature was a balmy minus 40 degrees Celsius and Fahrenheit; the scales cross at -40. The South Pole was warm and welcoming, homey, compared to Hilbert space.
Me at the South Pole in November 1992, early summer, when the sun never sets. It was minus 40 degrees, both Celsius and Fahrenheit. I had to keep blinking so my eyelids didn’t stick to my eyeballs. That’s my recollection, anyway.
Going Native
I’ve been watching a Netflix series on Scientology hosted by Leah Rimini, an actress and lapsed Scientologist. The series is really about the mystery of brainwashing. How could all these smart people get hoodwinked by this nutty, brutal cult? Brainwashing commandeers our attention. We’re told, over and over, This is what’s true, this is what matters, forget all that other stupid stuff you’ve learned. The wave function of your knowledge becomes as narrow as a Dirac delta function.
Cult-busters seek to deprogram cult members, to help them see through the cult’s lies. But deprogramming is just another form of programming. Ordinary citizens who disdain cults like Scientology embrace Catholicism or Islam or the meta-cult of money-obsessed, militaristic, mawkishly sentimental American culture. To be human is to be brainwashed.
Science is cultish, according to cranky old Thomas Kuhn. In The Structure of Scientific Revolutions, he says science cannot function without a paradigm, his term for a set of assumptions about how the world works and how science should investigate it. Paradigm is pretty close to ideology. Kuhn compares scientists under the sway of a paradigm to the brainwashed citizens in Orwell’s dystopian novel 1984. When you abandon your old scientific paradigm, like classical mechanics, you end up in the thrall of a new paradigm, like quantum mechanics.
Brainwashing is an offensive term for describing physics education. Going native is softer. Andrea Barrett wrote a haunting story, Servants of the Map, about going native. In the mid-19th century, a young, uptight English geographer goes on an expedition to the Himalayas to map mountains and collect plants. The story takes the form of letters from the geographer to his wife back in England. The letters chronicle the geographer’s evolution from homesickness and estrangement from the new world to entrancement with it. His old self dies, a new one is born. He is now estranged from everything in his old world, including his wife.
Science journalists go native when immersed in a field for a long time. You become so close to the experts, so immersed in their paradigm, that you over-identify with them; you have a hard time speaking to the non-experts who are your primary audience. I’m too old and dumb to go native. When it comes to physics, I will always be a mere journalist, an outsider. I can only imagine--. No, I cannot even imagine the fantastical symphony, accompanied by psychedelic laser-light show, playing in Edward Witten’s head as he contemplates the strings thrumming at the bottom of things.
N-Body Problems
As PEP553 winds down, Whittaker alludes to complexities we won’t deal with in this course. For the sake of simplicity, we haven’t confronted the effects of special relativity, and for the most part we’ve been looking at problems in only one or two dimensions. In the simplest version of the particle in a box, a particle moves back and forth along a line. Physics gets much harder as you add degrees of freedom. Much of what we’ve learned about particle behavior in one or two dimensions can be extended to three dimensions, Ed says. Quantum engineering depends, to a certain extent, on modeling the behavior of a particle in a tiny, three-dimensional box.
Ed tries once again to get us to appreciate the power of the Schrodinger equation. Before quantum mechanics, scientists could only speculate why hydrogen, when it burns, produces a unique spectrum, or pattern of light. The Schrodinger equation reveals—or should I say describes?—how a hydrogen atom generates its particular spectral lines. Hydrogen is a so-called two-body problem, consisting of a positively charged proton and negatively charged electron. The electron emits and absorbs lumps of electromagnetic radiation as it jumps from one energy level to another, hence the characteristic spectral lines.
Even two-body problems in classical mechanics can be horrendously hard to solve, Ed says, but there are tricks for turning a two-body problem into a one-body problem; the Schrodinger equation has special properties that enable this operation. Remembering something I’ve read, I ask Ed about helium: Can the Schrodinger equation give you an exact description of a helium atom? No, Ed replies, helium is not solvable with the Schrodinger equation, because you have a nucleus plus two electrons. Helium is a three-body problem. You can’t find exact solutions for three-body problems in either quantum or classical mechanics, although physicists have developed ways to attack these problems.
Ed’s response gives me a “Wait, what?” moment. I spend the next day googling the three-body problem. I had heard of it, but I had no idea how pervasive it is, and how old. Amerigo Vespucci and Galileo fussed over the three-body problem, but Newton gets the credit for identifying it in its modern form. He could not derive exact solutions to systems with three bodies, such as the Sun, Moon and Earth, with his laws of motion and gravity. Most three-body systems seem to be chaotic, unstable. They never reach equilibrium, a bound state; they scatter.
The three-body problem is a subset of the N-body problem, with N being any positive integer greater than one. The problem applies to interactions of objects of any kind, from electrons to stars. Solving three-body problems with general relativity is especially difficult; it’s hard to get exact solutions for even two bodies. Mathematicians have invented three-body systems that can be solved exactly, but it’s not clear whether these systems exist in nature. Physicists and mathematicians have devised methods for getting approximate solutions to N-body problems. These methods often generate “solutions” through brute force, number crunching.
But these methods take you further and further away from the elegance and simplicity of Newton’s laws, Coulomb’s law (which quantifies the force between two charged particles), the Schrodinger equation and general relativity. None of these famous formulas, by themselves, can account for even extremely simple features of nature. So why do physicists reify the equations, treating them as more real than the messy world in which we dwell?
Physicists say the Schrodinger equation describes our entire universe—or multiverse! But the equation doesn’t even provide an exact description of a helium atom, and it foists indeterminacy, the order-matters problem and other embarrassing conundrums on us. You might reasonably conclude that the Schrodinger equation is a tool with limited applications. Less charitably, it is a trick: mathematical skullduggery.
Galileo claimed that the book of nature “is written in mathematical language, and the letters are triangles, circles and other geometrical figures, without which means it is humanly impossible to comprehend a single word.” First of all, as my friend James McClellan, an historian of science who studied under Thomas Kuhn, likes to point out, there are no true triangles in nature. Nor are there any wave functions or Dirac delta functions, those infinitely thin, infinitely tall spikes with an area of one.
Second, the theory of evolution by natural selection is a pretty deep insight into nature, and Darwin laid it out in ordinary English without a single formula. Third, mathematics often gives us predictive power without insight, that is, competence without comprehension. Mathematics can’t help us solve many problems that matter to us, especially ones related to the strange creatures that Quark, a mischievous alien hustler in Deep Space Nine, the Star Trek spinoff, calls huuu-maanns.
In our next class, I tell Professor Whittaker I’ve been reading up on the three-body problem, and he asks what insights I’ve gleaned. I don’t lay my whole skeptical rant on him and my classmates. I just express surprise that the three-body problem is so pervasive; physicists need all these tricks to come up with approximate solutions for the problems. Yeah, that’s true, Ed says, chuckling. If it weren’t for the three-body problem, there wouldn’t be much for physics professors to teach; he’d probably be out of a job.
My research on the three-body problem freaks me out a little. How has the solar system, with all its planets and moons, remained in a stable, bound state for so long? Or the Milky Way, for that matter? Not to mention huuu-maann civilization, which consists of billions of bodies, each of which is unique. Maybe we’ve just had a streak of good luck, and it’s about to end.
Even two-body problems can be hard to solve exactly. This image, which I found on Wikipedia, shows factors affecting the orbit of a moon (A) around a planet (B). Imagine how complicated things get when two objects with free will orbit each other.
Wigner’s Reasonable Take on Physics
I find unlikely support for my sour musings in Eugene Wigner’s famous 1960 essay “The Unreasonable Effectiveness of Mathematics in the Natural Sciences.” I have resisted reading the essay, assuming it would be an annoying exercise in math-worshipping, chest-beating, physics triumphalism. I expected Wigner to argue that physicists’ mathematical models are revealing the Platonic truth behind the veil of things. To my surprise, his essay has the opposite message.
Wigner, who won a Nobel Prize for work in nuclear physics, begins by acknowledging that the equations embedded in Newton’s laws of motion, quantum mechanics and general relativity seem extraordinarily, even unreasonably effective. Why do they work so well? No one knows, Wigner says. But just because these models work, he emphasizes, does not mean they are “uniquely” true descriptions of nature. Wigner points out several problems with this assumption. First, theories of physics are limited in their scope; they apply only to specific, highly circumscribed aspects of nature, and they leave lots of stuff out.
Second, quantum mechanics and general relativity, the pillars of modern physics, are mathematically incompatible. “All physicists believe that a union of the two theories is inherently possible and that we shall find it,” Wigner writes. “Nevertheless, it is possible also to imagine that no union of the two theories can be found.” Sixty years after Wigner wrote his essay, quantum mechanics and relativity remain unreconciled. Doesn’t that imply that one or both are in some sense incorrect?
The “laws” of physics, Wigner adds, have little or nothing to say about biology, and especially about consciousness, the most baffling of all biological phenomena. When we understand life and consciousness better, inconsistencies might arise between biology and physics; these conflicts, like the incompatibility of quantum mechanics and general relativity, would mean that modern physics is incomplete or wrong. Here again Wigner—writing 60 years ago!--has proven prescient. Prominent scientists and philosophers—not just Deepak Chopra!—are questioning whether physics and indeed the basic paradigm of materialism can account for life and consciousness. Some claim that mind is at least as fundamental as matter.
Wigner urges his colleagues not to confuse their mathematical models with reality; just because a model works doesn’t mean it’s true. There may be different models that work just as well, or better. I like this message, perhaps because I work at an engineering school. Compared to physicists, engineers are humble. When trying to solve a problem--such as building a new car or drone--engineers don’t ask whether a given solution is true; they would see that terminology as a category error, like asking whether a heat-seeking missile is true. Engineers ask whether the solution works, meaning that it solves the problem at hand.
Mathematical models such as quantum mechanics and general relativity work extraordinarily well. But they aren’t real in the same sense that galaxies and planets and orchids are real, and we shouldn’t confer upon them the status of “truth” or “laws of nature.” If physicists adopt this humble mindset and resist their craving for certitude, they are more likely to seek and hence to find other unreasonably effective theories, perhaps ones that work even better than quantum theory. The catch is that they must abandon hope of finding a final, true formula that demystifies, once and for all, our weird, weird world.
Topologist’s Morning
Someone posts a joke on Facebook that feels like an addendum to Wigner’s “Unreasonable Effectiveness” essay. The joke is titled “Topologist’s Morning Routine.” Topologists are mathematicians who care about geometrical symmetries, properties that remain unchanged as you alter an object’s shape. A solid cube is the same as a solid sphere because you can massage the cube to get the sphere, or vice versa, without tearing a hole in it. If one of the objects has a hole, this symmetry is lost. Shape is superficial, holes are essential.
Funny, right?
“Topologist’s Morning Routine” consists of four captioned drawings of blobs with holes in them:
*“Cup of coffee” is a blob with one hole, formed not by the receptacle, which is an indentation that doesn’t matter to a topologist, but by the handle.
*”Pants” is a blob with two holes, for the legs.
*“Shirt” is a blob with three holes, for the neck and arms.
*“Socks” shows two blobs, one with no hole, the other with one hole.
The socks’ asymmetry stumps me until I realize that one sock has a hole in it. “Topologist’s Morning Routine” hits home, and not only because I’ve been dwelling on how math relates to the world. I’ve also become acutely conscious of the mathematical complexity of everyday tasks, like pulling on a t-shirt. The shirt depicted in “Topologist’s Morning” is too simple. Shirts are asymmetrical; they have a front and a back, corresponding to the front and back of the human body. Some of my t-shirts are so old that the tag on the back of the neck hole has worn away. If it lacks a pocket, I must eyeball the shirt to guess how to pull it on, and sometimes I guess wrong.
How would a topologist view a human body? Probably as a blob with one long hole extending from mouth to anus. Other holes—ears, nostrils, vagina, penile aperture—are pseudo-holes, indentations, like the cup of a teacup or pocket on a t-shirt. Once again, I’m reminded of the gap between reality and scientists’ mathematical models. As Wigner said, all models leave things out. The question is, do the omissions matter?
The topologist’s coffee cup doesn’t show the part that holds the coffee, and the sock omits what covers the foot. These omissions recall an old joke about a dairy farmer and a physicist: The farmer, hoping to make his farm more productive, asks the physicist for advice. The physicist says: Okay, first, let’s assume the cow is spherical, and it’s in a vacuum.
An effective model, like an artful synecdoche, omits a lot while capturing what’s important. If the model describes everyday things like cups and cows and people, we can judge for ourselves whether the model works. But physicists’ models often describe things remote from everyday experience, things that might not even exist. Quarks, strings, wave functions, black holes, parallel universes. Are the models leaving out something important, something that matters? Of course they are.
The End of PEP553
It’s the last week of PEP553, and Ed reviews topics likely to be on the final exam. I take notes, even though I’m not taking the exam. Possible topics include switching the basis of coordinate systems, deriving the hydrogen spectrum from the Schrodinger equation, calculating angular momentum. Angular momentum is crucial to physics at all scales, Ed says, from the very small to the very large. Electrons have a peculiar kind of angular momentum, embodied in their spin. Planets orbiting the Sun display conventional angular momentum. Kepler’s law, which says that planets orbiting the Sun sweep out areas at a constant rate, derives from conservation of angular momentum.
Speaking of planets, Ed says, Jupiter and Saturn will be in conjunction soon, which means that they will appear to be quite close in the sky. The last time this happened was early in the 13th century. There’s no record of that conjunction, but we know it happened because we can retrodict the planets’ orbits, which is amazing if you think about it. Yeah, I can see why physicists like Susskind believe in conservation of information. And the success of planetary predictions puts the three-body problem in its place.
If we continue studying quantum mechanics, Ed says, we’ll learn more about multi-particle quantum systems, which involve “a whole new level of complexity.” That will be covered in a physics course offered next spring. “Okay, that’s the end of the story,” Ed says. Story? What story? Looking up from my notebook, I realize that Ed means PEP553 is done; he has given his last lecture. I feel relief mixed with sadness.
Was PEP553 worth my investment of time and effort? Definitely. Ed Whittaker was a wonderful teacher, and PEP553 gave me a taste of what a real physics class and textbook are like. The Schrodinger equation is a little less strange to me. I have a better grasp of what wave functions are. I learned about the particle in a box, which is really a wave function in a box, and about non-commutation, the Dirac delta function and the N-body problem. I met my groovy study buddies, Dean and Luis.
But I’m not sure what I’ve learned, really. I didn’t hand in homework or take the exams, so I remain untested, in an uncertain state. Actually, that’s bullshit. There’s nothing uncertain about my state. I skipped most of the homework and both exams because I knew they would be too hard; I would have flunked. If my goal was to learn quantum mechanics the way a physics major does, to learn enough to pass PEP553, I failed, even though Ed did his best to help me. The question is, what do I do next? Is my quantum experiment over?
In the Beginning Was the Number
The gospel according to John says: “In the beginning was the Word, and the Word was with God, and the Word was God.” The gospel according to physics says: “In the beginning was the Number, and the Number was with God, and the Number was God.” The gospel of physics must be wrong. Numbers can’t represent the female huuu-maann sleeping in the next room, dreaming of… what? I’ll never know. Unless she wakes up and tells me, which she might.
When Emily gets up she asks, What have you been up to, Mr. Crazy Pants? I’m eager to tell her about my doubt that reality is mathematical. To lay the groundwork, I ask if she’s familiar with the phrase, “In the beginning was the Word…”
“Tree of Life,” a key concept of the Kabbalah, shows relations between different “emanations” of creation, represented by Hebrew letters and numbers. I found this image on Wikipedia.
That sounds like some Christian thing, says my girlfriend. Then she speaks very rapidly, as is her wont, especially in the morning, about the differences between the New and Old Testaments, about the Hebrew Bible and the Kabbalah, about Hebrew letters, which were derived from pictographs, like the letter for “word,” which looks like a flame and is also the letter for breath and spirit. Hebrew letters are associated with numbers, too…
That’s very interesting, I interject, because I was just writing about physicists’ belief that reality is mathematical. Physicists are saying, essentially: In the beginning was the Number…
Emily interrupts to tell me that when she was 13, she spent a summer working in a jewelry store. The store displayed rings in velvet cases. When the owner took a ring from a slot in the velvet case, he put a penny in the slot as a placeholder. That’s all numbers are, Emily says, placeholders. They’re not real; they only stand for real things, in the same way that money stands for things with value, like food or land or diamond rings.
I mull over Emily’s placeholder theory of math. Some things become real, they matter, because we believe in them. Like money, justice, democracy and the United States of America. Other things exist whether or not we believe in them. Like water, mountains, planets and galaxies. Philip Dick said, “Reality is that which, when you stop believing in it, doesn’t go away.” Do other people exist when we stop believing in them? Yes. What about the Schrodinger equation? No, even though the equation works. Is an electron still there if we stop believing in it? That’s a harder question to answer.
Quantum Notebook #3, notes from final session of PEP553, December 10, 2020.
I brief Emily on the N-body problem. I tell her that if physicists can’t model a helium molecule exactly, they can’t possibly model her. I mean this as a compliment, and she takes it as such. Yes, my girlfriend concurs, she is extremely complicated. Then she says, You’d be much easier to model than me.
I’m a little offended. Modeling me would be hard, too, I object, because of my fondness for irony, for saying things with more than one meaning. She replies that when I’m being “ironic”—she brackets the word in scare quotes--I’m usually just being passive-aggressive. My reflexive reaction to her critique is, Wrong! But after brooding for a while, I grudgingly admit--to myself, not to her--that maybe she’s right.
Emily always knocks me for a loop. Whatever I predict will happen when we interact rarely does. We form an unstable two-body system. For 12 years we’ve been orbiting each other, loosely bound, simultaneously attracted and repelled, never achieving equilibrium or harmony. Trajectories recur but never precisely. We will keep tumbling toward and away from each other until one of us departs or dies, leaving the other to drift alone in unbounded space.
Notes
No notes here! Move on!
Table of Contents
INTRODUCTION
Old Man Gets More Befuddled
CHAPTER ONE
The Strange Theory of
You and Me
CHAPTER TWO
Laziness
CHAPTER THREE
The Minus First Law
CHAPTER FOUR
I Understand That
I Can’t Understand
CHAPTER FIVE
Competence Without Comprehension
CHAPTER SIX
Reality Check
CHAPTER SEVEN
The Investment Principle
CHAPTER EIGHT
Order Matters
CHAPTER NINE
The Two-Body Problem
CHAPTER TEN
Entropy
CHAPTER ELEVEN
The Mist
CHAPTER TWELVE
Thin Ice
CHAPTER THIRTEEN
Irony
EPILOGUE
Thanksgiving