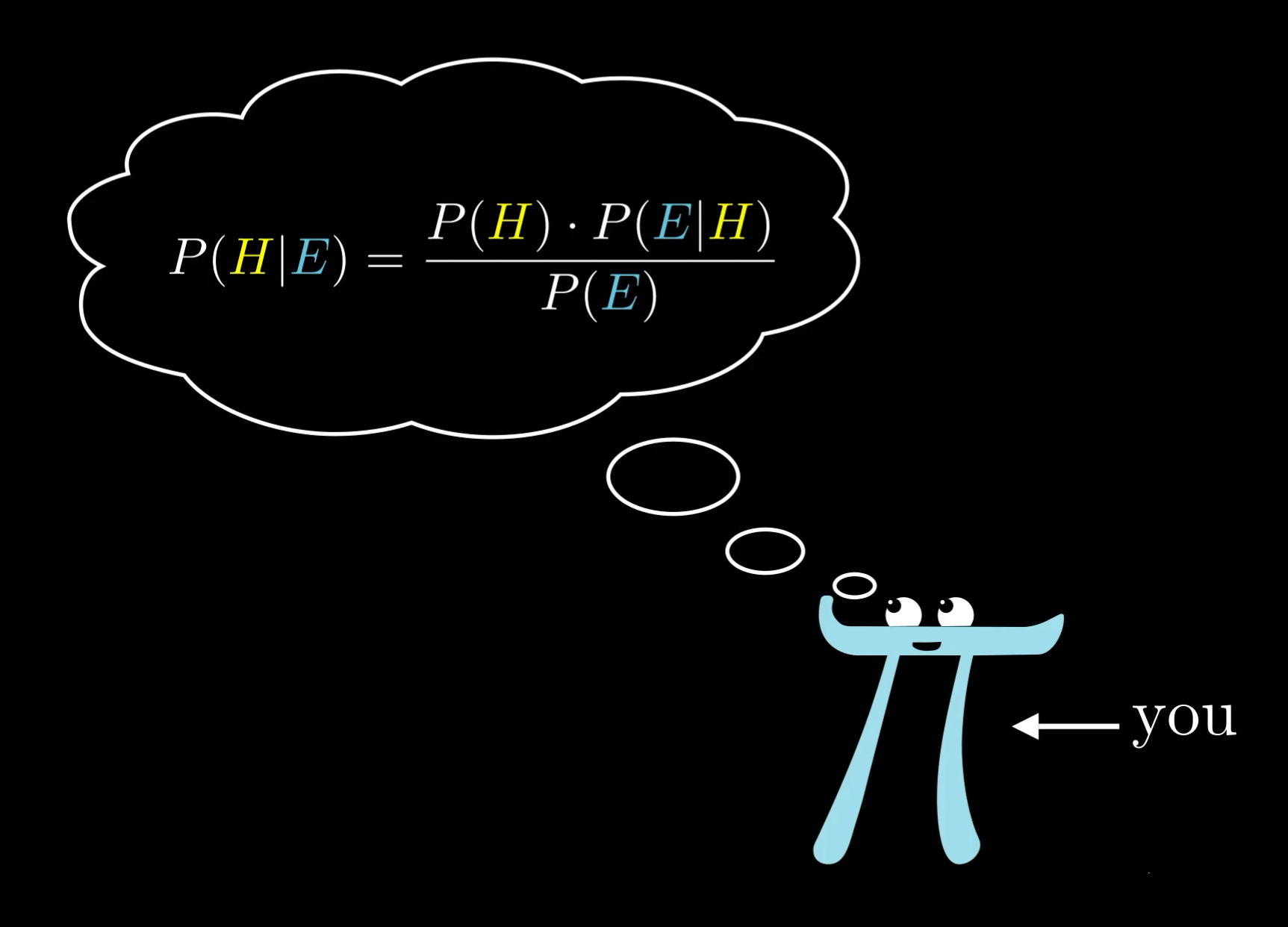Bayes’ Theorem and Bullshit
The website 3blue1brown.com has terrific tutorials on all sorts of mathematical topics, including Bayes’ theorem.
January 5, 2024. A while back one of my students, “Frank,” a real smarty-pants, started babbling about something called Bayes’ theorem. He wrote a long, dense paper about the theorem’s revelatory power, which had changed the way he looked at life.
The grandiose claims Frank made for Bayes’ theorem couldn’t possibly be true. A formula for reliably distinguishing truth from bullshit? Come on, give me a break. I dismissed Bayes’ theorem as a passing fad, like Jordan Peterson, not worth deeper investigation.
But I kept bumping into Bayes. Researchers in physics, neuroscience, artificial intelligence, social science, medicine, you-name-it are using Bayesian statistics, Bayesian inference, Bayesian whatever to model things and solve problems. Scientists have proposed Bayesian models of the brain and Bayesian interpretations of quantum mechanics. The math website 3blue1brown.com (where I found the image above) calls Bayes’ theorem “central to scientific discovery.”
I reluctantly decided to give Bayes a closer look, to see what the fuss is all about. In this column, I’ll explain how Bayes’ theorem works and, more broadly, what it means, and I’ll bold my main takeaways. I trust kind readers will, as usual, point out my errors. Here goes:
Named after its 18th-century inventor, Presbyterian minister Thomas Bayes, Bayes’ theorem is a method for calculating the validity of hypotheses (aka claims, propositions, beliefs) based on the best available evidence (aka observations, data, information). Here’s the most dumbed-down description: Tentative hypothesis plus new evidence = less tentative hypothesis.
Here’s a fuller version: The probability that a hypothesis is true given new evidence equals the probability that the hypothesis is true regardless of that new evidence times the probability that the evidence is true given that the hypothesis is true divided by the probability that the evidence is true regardless of whether the hypothesis is true.
Got that? Okay, let me unpack it for you. Bayes’ theorem takes this form: P(H|E) = P(H) x P(E|H) / P(E), with P standing for probability, H for hypothesis and E for evidence. P(H) is the probability that H is true, and P(E) is the probability that E is true. P(H|E) means the probability of H if E is true, and P(E|H) is the probability of E if H is true.
Medical testing often serves to demonstrate the formula. The hypothesis, H, is that you have a disease. You want to know what the odds are that this hypothesis is correct given evidence, E, such as a positive test for the disease. Your odds are represented by P(H|E), the probability that you have the disease given a positive test.
Let’s say you get tested for a cancer estimated to occur in 1 percent of the population. If the test is 100 percent accurate, you don’t need Bayes’ theorem to know what a positive test means, but let’s use the theorem anyway, just to see how it works.
You plug your data into the right side of Bayes’ equation. P(H), the probability that you have cancer before getting tested, is 1 percent, that is, 1/100, or .01. P(E), the probability that you will test positive, is also .01. Because P(H) and P(E) are in the numerator and denominator, respectively, they cancel each other out, and you are left with P(H|E) = P(E|H) = 1.
That means the probability that you have cancer if you test positive is 1, or 100 percent, and the probability that you test positive if you have cancer is also 1, or 100 percent. More succinctly, if you test positive, you definitely have cancer, and vice versa.
In the real world, tests are rarely if ever totally reliable. Let’s say your test is 99 percent accurate. That is, 99 out of 100 people who have cancer will test positive, and 99 out of 100 who are healthy will test negative. That’s still a terrific test. If your test is positive, how probable is it that you have cancer?
Now Bayes’ theorem displays its power. Most people assume the answer is 99 percent, or close to it. That’s how reliable the test is, right? But the correct answer, yielded by Bayes’ theorem, is only 50 percent.
Plug the data into the right side of Bayes’ equation to see why. P(H) is still .01. P(E|H), the probability of testing positive if you have cancer, is now .99. So P(H) times P(E|H) equals .01 times .99, or .0099. This is the probability that you will get a true positive test, which shows you have cancer.
What about the denominator, P(E)? Here is where things get tricky. P(E) is the probability of testing positive whether or not you have cancer. In other words, it includes false as well as true positives.
To calculate the probability of a false positive, you multiply the rate of false positives, which is 1 percent, or .01, times the percentage of people who do not have cancer, .99. The total comes to .0099. Yes, your terrific, 99-percent-accurate test yields as many false positives as true positives.
Let’s finish the calculation. To get P(E), add true and false positives for a total of .0198, which when divided into .0099 comes to .50. So once again, P(H|E), the probability that you have cancer if you test positive, is only 50 percent.
If you get tested again, you can reduce your uncertainty enormously, because your probability of having cancer, P(H), is now 50 percent rather than 1 percent. If your second test also comes up positive, Bayes’ theorem tells you that your probability of having cancer is 99 percent, or .99.
As this example shows, iterating Bayes’ theorem can yield precise information. But if the reliability of your test is 90 percent, which is still pretty good, your chances of actually having cancer even if you test positive twice are still less than 50 percent.
Most people, including physicians, have a hard time understanding these odds, which helps explain why we are overdiagnosed and overtreated for cancer and other disorders (see Further Reading). This example suggests that Bayesian enthusiasts are right: the world would indeed be a better place if more people—or at least more health-care providers and consumers--adopted Bayesian reasoning.
On the other hand, Bayes just codifies common sense. Consider the cancer-testing case: Bayes’ theorem says your probability of having cancer if you test positive is the probability of a true positive test divided by the probability of all positive tests, false and true. In short, beware of false positives.
Here is my more general statement of that principle: The plausibility of your hypothesis depends on the degree to which your hypothesis--and only your hypothesis--explains the evidence for it. The more alternative explanations there are for the evidence, the less plausible your hypothesis is. That, to me, is the essence of Bayes’ theorem.
“Alternative explanations” can encompass many things. Your evidence might be erroneous, skewed by a malfunctioning instrument, faulty analysis, confirmation bias, even fraud. Your evidence might be sound but explicable by many hypotheses other than yours.
In other words, there’s nothing magical about Bayes’ theorem. It boils down to the truism that your hypothesis is only as valid as its evidence. If you have good evidence, Bayes’ theorem can yield good results. If your evidence is flimsy, Bayes’ theorem won’t be of much use. Garbage in = garbage out.
The potential for Bayes abuse begins with P(H), your initial estimate of the probability of your hypothesis, often called the “prior.” In the cancer example above, we were given a nice, precise prior of 1 percent, or .01, for the prevalence of cancer. In the real world, experts disagree over how to diagnose and count cancers. Your prior will often consist of a range of probabilities rather than a single number.
In many cases, estimating the prior is just guesswork, allowing subjective factors to creep into your calculations. You might be guessing the probability of something that--unlike cancer—might not even exist, such as wormholes, multiverses or God. You might then cite dubious evidence to support your dubious hypothesis. In this way, Bayes’ theorem can promote pseudoscience as well as reason.
Embedded in Bayes’ theorem is a moral message: If you aren’t scrupulous in seeking alternative explanations for your evidence, the evidence will just confirm what you already believe. Even more simply: Doubt yourself. Scientists often fail to heed this dictum, which helps explains why so many scientific claims turn out to be erroneous. Bayesians claim their methods can help scientists overcome confirmation bias and produce more reliable results, but I have my doubts.
Physicists who espouse string and multiverse theories have embraced Bayesian analysis, which they apparently think can make up for lack of genuine evidence. The prominent Bayesian statistician Donald Rubin has served as a consultant for tobacco companies facing lawsuits for damages from smoking. As the science writer Faye Flam once put it, Bayesian statistics “can’t save us from bad science.”
The next time someone like Frank, my former student, gushes to me about Bayes’ theorem, I’ll say: Yeah, it’s a cool tool, but what it really means--and I’m just guessing here, don’t take my word for it--is that we should never be too sure about anything, including Bayes’ theorem. The claim that Bayes’ theorem can protect us from bullshit is, well, bullshit.
Note: This is a streamlined, updated, vastly improved version of a paywalled piece I wrote for Scientific American.
Further Reading:
There’s lots of great stuff on Bayes’ theorem online, some of which I’ve linked to above. See also Wikipedia’s entry, the Stanford Encyclopedia of Philosophy entry, the website of statistician Andrew Gelman, this tongue-in-cheek-but-still-serious essay by Eliezer Yudkowsky (which Yudkowsky insists has been superseded by this website) and the tutorial of the math website 3blue1brown.com (where I found the image above).
See also Pluralism: Beyond the One and Only Truth; and Chapter Five of my book My Quantum Experiment, which delves into a Bayesian interpretation of quantum mechanics.
And let’s not forget my last column, Self-Doubt Is My Superpower, and my 2023 columns on cancer: Mammography Screening Is a Failed Experiment, Do Colonoscopies Really Save Lives?, We’re Too Scared of Skin Cancer, The Cancer Industry: Hype Versus Reality.